Least Squares

This is note1 based on Linear Algebra And Learning From Data by Gilbert Strang.

---

Least Squares

Many applications lead to unsolvable linear equations $Ax=b$. The least squares method chooses $\hat x$ to make $||b-A\hat x||^2$ as small as possible. Which is $(Ax-b)^T(Ax-b)$. Minimizing erorr means its derivatives are zero which leads to normal eqautions $A^TA\hat x=A^Tb$.

Four ways to solve

1.The SVD of A leads to its pseudoinverse $A^+$. Then $\hat x = A^+b$ :one short formula (This note)
2.$A^TA\hat x=A^Tb$ can be solved directly when A has independent columns
3.The Gram-Schmidt idea produces orthogonal columns in Q which is $A=QR$. 4.Minimize $||b-Ax||^2 + \delta^2||x||^2$

$A^+$ is Pseudoinverse of A

Recall from four subspaces

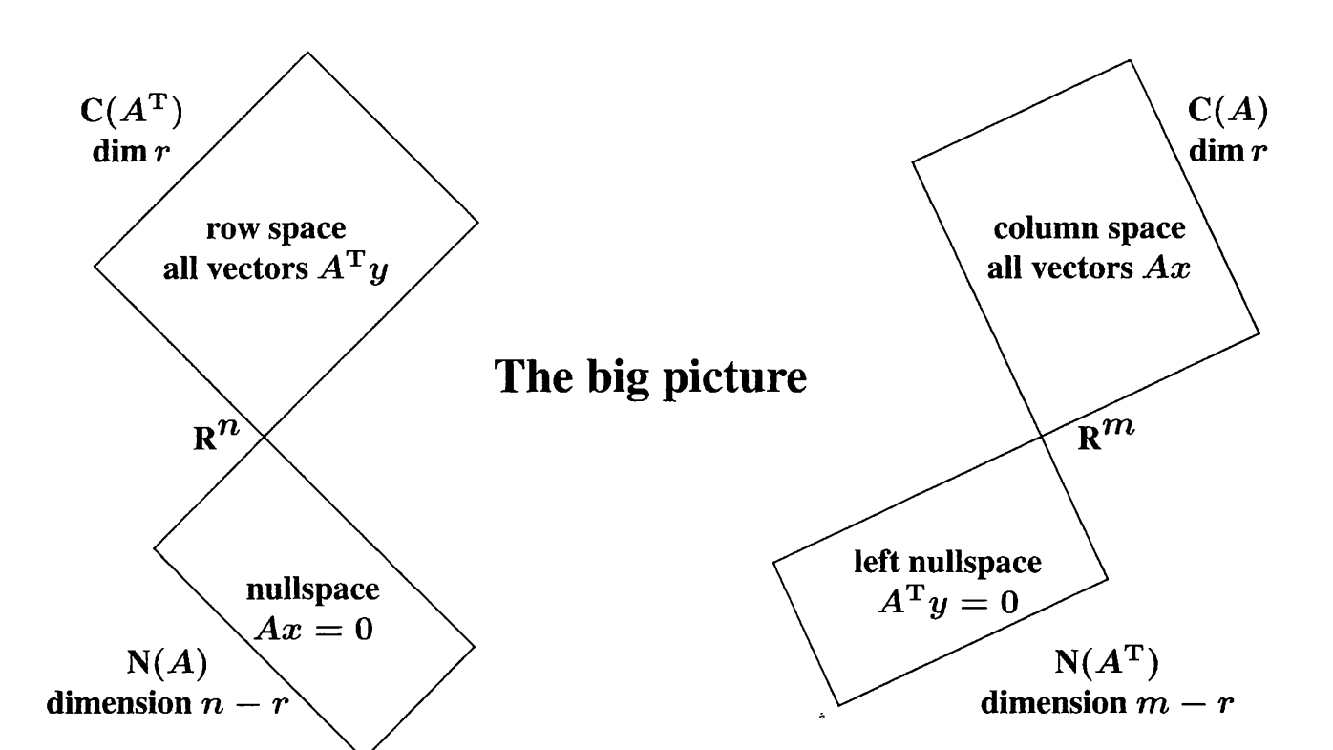
When A multiplies a vector x in its rowspace (otherwise Ax = 0), this produces Ax in the column space. If A is invertible, then $A^+ =A^{-1}$, and we have $A^+Ax=x$ exactly when x is in the row space. And $AA^+b=b$ when b is in the column space.
We conclude:
$A$: Row space to column space
$A^+$: Column space to row space

Rules to get pseudoinverse

1. If A has independent columns, then $A^+=(A^TA)^{-1}A^T$ and $A^+A=I$
2. If A has independent rows, then $A^+=A^T(AA^T)^{-1}$ and $AA^+=I$
3. A diagonal matrix $\sum_{mn}$ has $\sum ^+ _{nm}$

for all matrices: $A=U\sum V^T$ (SVD) , $A^+=V\sum^+U^T$

The Least Squares Solution to $Ax=b$ is $x^+ = A^+B$

properties:
$x^+=A^+b$ makes $||b-Ax||^2$ as small as possible.
If another $\hat x$ achieves then $||x^+||\le||\hat x||$ (Minimum norm)

Hanqing Shi

Curently study in University of Electronic Science and Technology of China(UESTC).

Comments

  Write a comment ...