Statistics Note1
This is note1 based on Linear Algebra And Learning From Data by Gilbert Strang.
1.Big picture
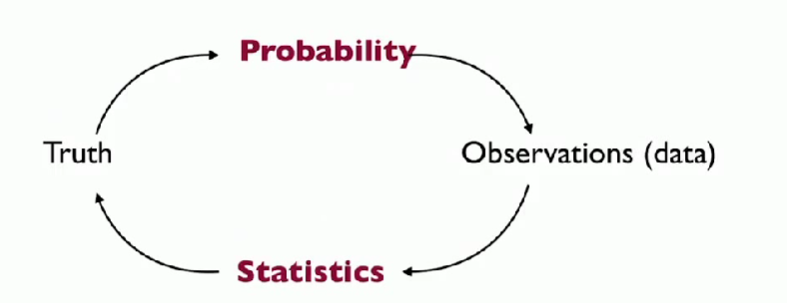
When an ouput is predicted, we need its probability. When that output is measured,we need its statistics.
2.Mean,Variance
Sample mean : $m=\mu=\frac{1}{N}(x_{1}+x_{2}+\cdots+x_{N})$
Expected Value : $m=E[x]=p_{1}x_{1}+p_{2}x_{2}+\cdots+p_{n}x_{n}$
Law of Large Numbers: $\mu\to E[x]$ , as N increases.
Sample Variance:
$S^{2}=\frac{1}{N-1}[(x_{1}-m)^2+(x_{2}-m)^2+\cdots +(x_{N}-m)^2]$
Variance: $\sigma^2=E[(x-E[x])^2]=p_1(x_1-m)^2+p_2(x_2-m)^2+\cdots +p_n(x_n-m)^2$
The variance $\sigma ^2$ measures the expected distance(squared) from the expected mean E[x].
The sample variance measures actual distance(squared) form the actual sample mean $\mu$.
Notice! : the denominator in sample variance is N-1,so that $S^2$ is unbiased estimate of $\sigma^2$. (Bessel’s Correction)
Proof:\(E[S^2]=E[\frac{1}{N-1}\sum(x_i-m)^2]=\frac{1}{N-1}E[\sum x_i^2-2\sum x_im+\sum m^2] \\=\frac{1}{N-1}E[\sum x_i^2-Nm^2]=\frac{1}{N-1}[E[\sum x_i^2]-E[Nm^2]]\)
Notice that:
\(\begin{align*}
E[\sum x_i^2] &= \sum E[x_i^2] \\
&= \sum (var(x_i)+E[x_i]^2) \\
&= N(\sigma^2 +\mu^2)
\end{align*}\)
similarly:
\(\begin{align*}
E[Nm^2] &= N E[m^2] \\
&= N(var(m)+E[m]^2) \\
&= N(\frac{1}{N}\sigma^2+\mu^2)
\end{align*}\)
Therefore:
$$E[S^2]=\frac{1}{N-1}[(N-1)\sigma^2]=\sigma^2$$
3.Probability Distributions
| distribution |
description |
| Binomial |
Tossing a coin n times |
| Poisson |
Rare evernts |
| Exponential |
Forgetting the past |
| Gaussion |
Averages of many tries |
| Log-normal |
Logaithm has normal distribution |
| Chi-squared |
Distance squared in n demensions |
| Multivariable Gaussian |
Probabilities for a vector |
Binomial
\(\mu = np,\sigma^2=np(1-p)\)
Poisson
\(p\to0,n\to\infty,np=\lambda\)
binomial
$p_{0,n}=(1-p)^n=(1-\frac{\lambda}{n})^n\to e^{-\lambda}$
$p_{1,n}=np(1-p)^{n-1}=\frac{\lambda}{1-p}(1-\frac{\lambda}{n})^n\to \lambda e^{-\lambda}$
Poisson probability
\(P_k=\frac{\lambda ^k}{k!}e^{-\lambda}\)
\(\mu=\lambda,\sigma^2=\lambda\)
Exponential distribution
It describes the waiting time in a poisson process.(continous,memoryless)
\(p(x)=\lambda e^{-\lambda x}(x\ge 0) ,F(t)=1-e^{-\lambda t}\)
\(\mu=\frac{1}{\lambda},\sigma^2=\frac{1}{\lambda ^2}\)
Chi-squared Distribution
\(\chi ^2_{n}=\sum x_{i}^2\)
where $x_{i}$ are independent standard normal r.v.
The Gamma function
\(\Gamma(n)=(n-1)!\).
Typical use :
$S^2$ is a sum of squares with $n-1$degree freedom. It has the probability distribution $p_{n-1}$for $\chi_{n-1} ^2$
Example:
\(for\ n=2,S^2=\frac{1}{2}(x_1-x_2)^2\)
Hanqing Shi
Curently study in University of Electronic Science and Technology of China(UESTC).



Comments